



Looking
for the GREATEST monomial factor:
(one variable please...level 1)
Now you know that monomials can be broken down into their various factors, and this is called "factoring monomials". We can proceed a bit further and begin to find common factors in POLYNOMIALS.
Actually, we will go so far as to find the GREATEST COMMON MONOMIAL FACTOR of every monomial in the polynomial. Once this is found, we will divide it out of each monomial term.
It's kind of like solving a puzzle. You will be looking for the biggest missing piece that is common to all the given parts.
Here, let's take a look at one:
Ex 1: Find the greatest common monomial factor of this polynomial, divide it out, and rewrite the polynomial as a multiplication problem using the factors you found.
![]()
Now look at these three terms. Is there a factor that will divide EVENLY into ALL THREE? If you can find one, it will be a called a "common" factor. Then all we have to do is make sure that it is the GREATEST common factor.
After a bit of looking, we see that the number 3 will divide into all three terms. However, we can't find anything else that will divide into all three terms. So 3 must be the GREATEST common factor.
When we divide three out of each term and then rewrite as a multiplication problem it will look like this:
![]() .
.
Ex 2: Factor
the polynomial ![]() into the product of its greatest monomial factor and another trinomial.
into the product of its greatest monomial factor and another trinomial.
Here the numerical coefficients on each term are all even so 2 will definitely divide into them all without a remainder.
Also, we see that there is a power of "n" in each term. The smallest exponent in all three terms is the understood 1 on the last term, so "n" will divide evenly into each term along with the 2 found above. That makes the GREATEST common factor for this example "2n".
When we divide it out and rewrite the polynomial as a product of its greatest common factor and another trinomial it will look like this:
![]()
*NOTE: You can always check your factored answer by simply multiplying it. If you don't get the original polynomial back, you know you are wrong.
Give these three a try. Write down your answers before you click the answer link.
Factor each trinomial into a product of its greatest monomial factor and another trinomial.
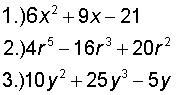
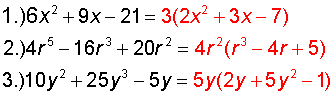
Looking
for the GREATEST monomial factor:
(two variables allowed now...level 2)
Try these using the same technique as the one variable, greatest common monomial factoring.
Write down what you think the "factored forms" will look like, then click the ANSWERS link to see if you are correct.
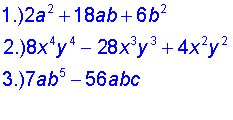
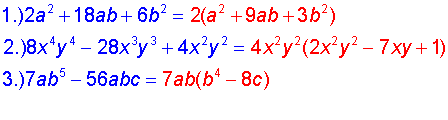
Home | About
Us | Algebra| Dictionary | Games | Geometry | Gym | Humor | Lab | Magic | Natural Math | PreAlgebra | Resources | Teachers Only | Toolbox | Treasures | Videos | Wonders | Writings |
Copyright © 1999-2020 themathlab.com
