|
As time went on, the
Pythagoreans
made even more exciting discoveries-and gave them strange cosmic meanings.
This curious blend
was characteristic of Pythagorean geometry. For the initiates of the Brotherhood
were seeking a special key to the universe in this wonderful new realm
of numbers and abstract forms: triangles, circles, squares, spheres, and
the more elaborate forms they made themselves.
And their search had
a thrilling climax. After long and painstaing experiments, they discovered
the five regular solids. These were remarkable and beautiful polyhedrs,
or shapes with many faces.
The full tale of these
five solids can only be guessed at from bits of legend and history, for
all the experiments were top secrets, of course.
To impress this on
newcomers, perhaps the first thing they were shown was how to make a mystic
"pentagram," the emblem that members of the Order wore on their
clothing. By means of a secret device ( which we will explain later) a
five-sided figure, or pentagon, was traced on cloth. Then its points were
connected with diagonals to make a five-pointed star. Finally, around
the five points of the star were placed the letters of the Greek work
for health, (hygeia), from which we get the word "hygiene".
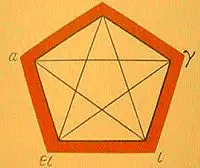
This was the sacred
symbol of the Pythagorean
Order - the "magic pentacle" that remained a favorite device
of sorcerers and conjurors for many centuries. But it was also an experimental
discovery: The first known use of letters on a geometric figure.
Possibly the next
experiment shared with newcomers was a basic one with tiles. Ordinary
floor tiles had yielded the easiest example of the Pythagorean theorem.
So the Secret Brotherhood went on with a painstaking study of these close-fitting
forms that covered many Greek floors.
They made loose tiles
of variious shaped and placed them in patterns on the ground. And they
reached a striking conclusion. There were only three regular shapes
of tiles that would fit together perfectly to cover a flat area completely:
triangles ( three sides), squares (four sides), hexagons (six sides).

If they tried pentagons,
they got a beautiful blossomlike design, but there were gaps between the
tiles, and tiles of more than six sides would always overlap. No other
regular geometric forms of the same size and shape could be so combined.
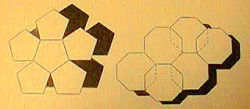
They explained this
mystery to the newcomers: "Since there are four right angles (360
degrees) around a point, you can only use forms whose corner angles together
will make that total. There are just three possibilities: six equilateral
triangles with 60 degree angles, four squares with 90 degree angles, and
three hexagons with 120 degree angles."
From this simple experiment
came the fascinating idea of making "solid angles" by fastening
tiles together with mortar, or gluing together shapes of wood, or sewing
together pieces of leather. And this led to building shapes with the solid
angles.
They called them regular
solids because all the edges and faces and angles in each solid were
equal. And after much experimenting, as we have said, they found five
of these solids. The first two had been known from the most ancient times,
but the next two were shapes that men had never seen before. As for the
fifth, it was such a startling discovery that they thought they had upset
the order of the universe!
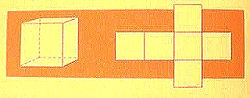
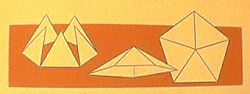
The Cube: They
mortared three square tiles into an angle, and fitted on three more tiles
to form a cube with six square faces, which they called a hexahedron.
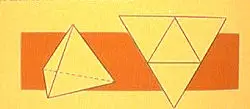
The Regular Pyramid:
They put together three equilateral triangles into a solid angle,
then added one more, to make the base of their four-faced tetrahedron.
The Octahedron:
This was made with two solid angles of four equilateral triangles each,
so they gave this eight-faced figure the name octahedron.
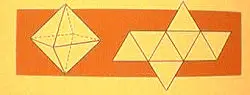
The Icosahedron:
Here was a real challenge. When they put together five equilateral
triangles, they got a surprise. The open base of this solid angle
was a pentagon. Now they could trace one perfectly for their emblem,
instead of just drawing it freehand. (Of course, the device was kept secret.)
But how could they make a regular solid, with five equilateral triangles
around each vertex? All their early attempts were failures.
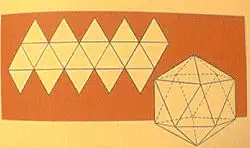
Finally, someone
got the right inspiration-five equilateral triangles for the top, and
five triangles for the bottom, and then a center band of ten more tianles
based on the old Babylonian pattern. They had made an icosahedron
with twenty triangular faces.
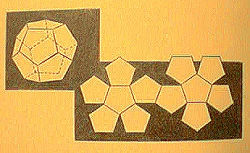
The Dodecahedron:
This last form was made with the pentagons so dear to the Pythagorean
Order. They used that flowerlike pattern of a single pentagon surrounded
by five others-the tiles that would not fit together on the flat floor.
But if the surrounding ones were lifted up, then all six pentagons fitted
perfectly in a solid cuplike shape. This could be capped by an inverted
one just like it to yield the most difficult and beautiful of the five
regular solids: the dodecaheron with its twelve pentagonal faces.
These five shapes
created a great stir among the first geometers who studied them. Men examined
them in fascination and awe, handling them, turning them around in different
positions, looking through them as if they were glass. And it was inevitable
that the Pythagoreans should finally give them mystical meanings.
By the time the Secret
Brotherhood had spread to many towns and islands of Sicily and southern
Italy. The Sicilian members were friendly with another strange teacher
who lived near Mount Etna- Empedocles, who dressed all in purple, gave
away his money, and did scientific experiments.
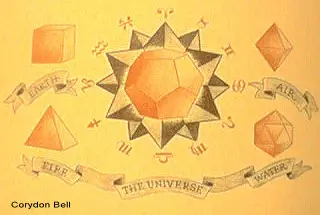
Empedocles taught
that the world was made of earth, air, fire, and water, and the first
four regular solids came to be identified with these "elements."
We know the identification from a famous passage in one of Plato's Dialogues,
where it is made by a Pythagorean from Locri in the south of Italy. About
the fifth solid, there were many weird stories. Its existence was kept
secret as it seemed to require a fifth "element."
The esoteric reasoning,
as repeated later, went something like this:
"The cube, standing
firmly on its base, corresponds tot he stable earth. The octahedron, which
rotates freely when held by its two opposite corners, corresponds to the
mobile air.
"Since the regular
pyramid has the smallest volume for its surface, and the almost spherical
icosahedron the largest, and these are the qualities of dryness and wetness,
the pyramid stands for fire and the icosahedron for water."
As for the last-found
regular solid, with its twelve faces, "Why not let the dodecahedron
represent the whole universe, since the Zodiac has twelve signs!"
Such notions were
typical of that age. And more than two thousand years later, the famous
astronomer Kepler was still so awed by the unique properties of the five
regular solids that he tried to apply them as planetary orbits: he assigned
the cube to Saturn, the pyramid to Jupiter, the dodecahedron to Mars,
the icosahedron to Venus, and the octahedron to Mercury, and he designed
a machine to show this! Of course, the attempt was a failure.
Yet even today, these
solids seem almost magical in their beauty and their interrelations.
in the first place,
it is quite startling that there are only five. An infinite number of
regular polygons can be inscribed in a circle-their sides becoming so
small that they approach the form of the circle itself. But it is not
so with regular convex polyhedra inscribed in a sphere. There are only
these five posible shapes, and no others.
And these five shapes
are connected with one another in a most remarkable way. All five can
be fitted together, one inside the next, like the compartments of some
magic box. And they are further linked by a strange inner harmony. They
can be inscribed in themselves or each other, in certain endless thythmic
alternations. So it's no wonder the five regular solids were long referred
to as the "dice of the gods."
|

 The tetrahedron or "regular pyramid".
The tetrahedron or "regular pyramid". The cube, sometimes called
a "hexahedron".
The cube, sometimes called
a "hexahedron". The octahedron.
The octahedron. The icosahedron.
The icosahedron. The famous dodecahedron.
The famous dodecahedron.




